
75
9. Derivasjon - Med spillkort
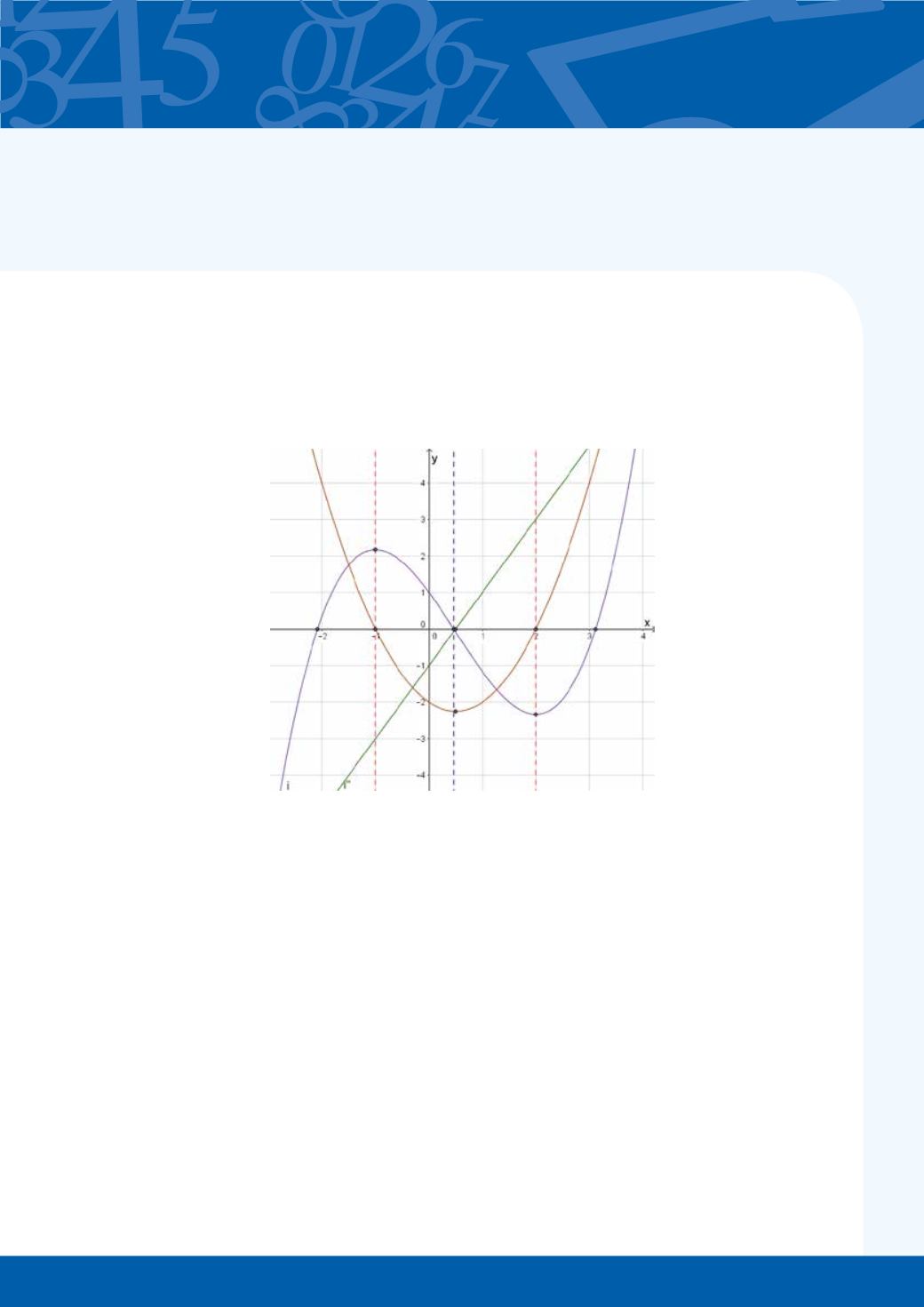
Etter litt jobbing med spillkortene vil elevene få mange erfaringer med å se sammenhengene mellom
et funksjonsuttrykk, den førstederiverte og den andrederiverte. Det kan da være spennende å lage
en animasjon med glidere i GeoGebra der alle tre grafene presenteres samtidig. Elevene vil da se de
sammenfallende
x
-verdiene for alle tre uttrykkene. Se forklaring på GeoGebra-veiledningen til dette
heftet på
www.matematikksenteret.no.
UTVIDELSE AV OPPGAVEN
En del elever motiveres av at oppgavene har et konkurransemoment. Oppgaven med spillkort kan
enkelt endres slik at to og to elever konkurrerer mot hverandre. Konkurransen går ut på at de to
elevene raskest mulig skal nne est tripler med kort. Elevene trenger ikke å bruke spillbrettet. Sørg
for at elevene begrunner hvorfor løsningene er riktige.
La elever som trenger en ekstra utfordring lage nye spillekort. Da blir elevene utfordret til å tenke
oppgaven «bakvendt».
Det er også mulig å lage en liten vri på oppgaven, men fortsatt bruke kopieringsoriginalene. I stedet
for å ha funksjonsuttrykkene bakpå kortene, kan de kopieres på egne kort. Oppgaven blir da å nne
de re kortene som hører sammen (kvartett).

















