
30
4. Figurtall, følger og rekker - Treet
Grenseverdien ved regning:
Dette er en god repetisjon av algebra. Dersom man skal nne grenseverdien ved regning, ligger
vanskeligheten i å omforme 2
n+1
slik at brøken kan forkortes.
1
1
2 1
2 1
2 2 1
1
lim
lim
lim
2 lim 2
2
2 2
2 2
2
n
n
n
n
n
n
n
n
n
n
n
n
n
+
+
→∞
→∞
→∞
→∞
−
⋅
=
− =
− = −
=
Grenseverdien som sum av en uendelig geometrisk rekke
Den samlede lengden øker med:
Den totale lengden er en geometrisk rekke med
k =
og a
1
= 1
1
1 2 1
1 1
2
a s
k
= = =
− −
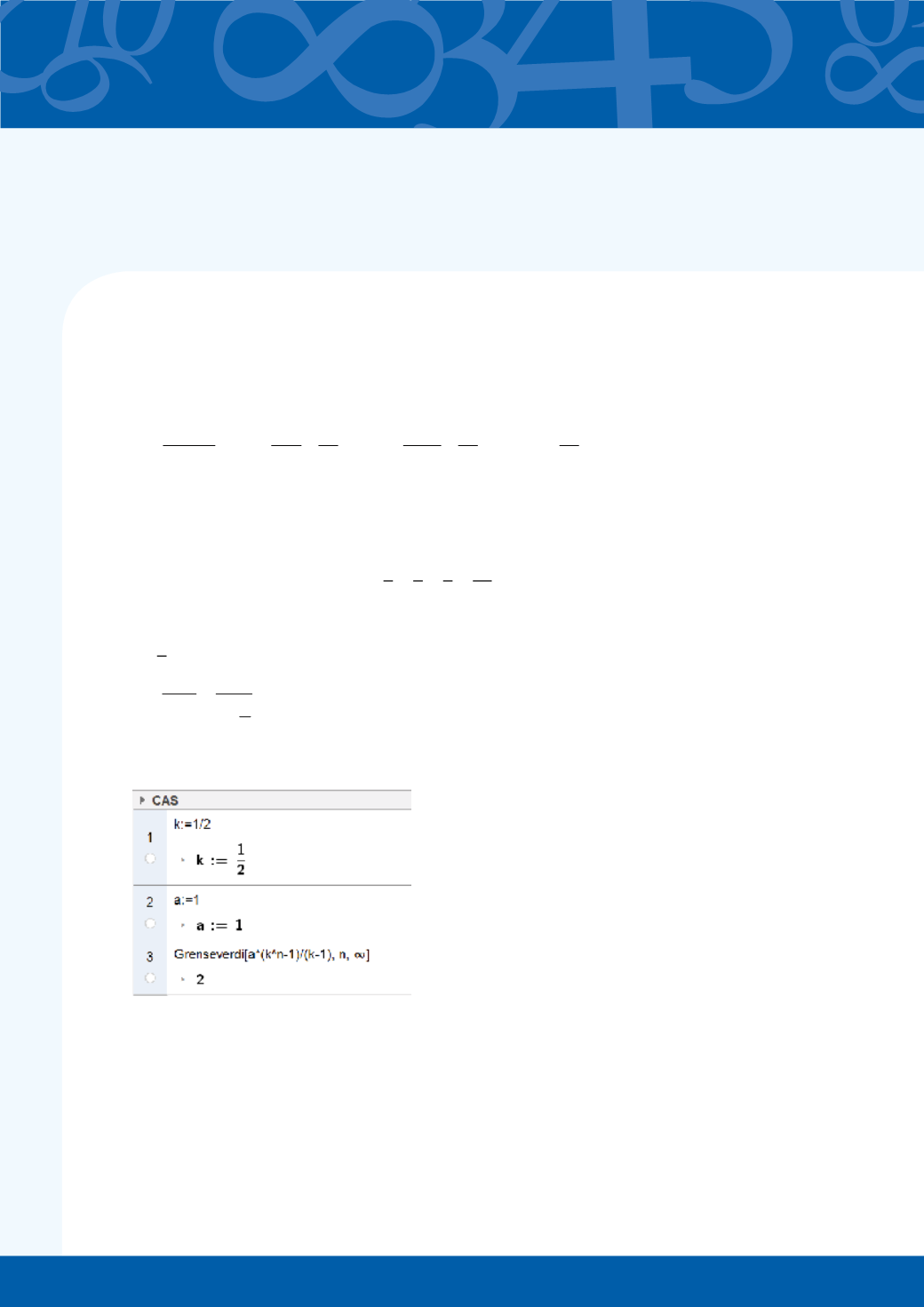
Ved grenseberegning med CAS nner man samme svar.
Denne oppgaven er velegnet som repetisjonsopplegg i R2. Oppgaven viser at man kan få samme svar
på mange ulike måter. Det er viktig at elevene får anledning til å diskutere de ulike løsningsmåtene.
Gjennom klassesamtaler vil elevene se at de ulike delene av læreplanen henger sammen, og for
mange elever er dette en aha-opplevelse. Når de får anledning til å re ektere over svarene, vil mange
elever oppleve at læresto et henger sammen.
� ∙ (� − �) ∙ � � + �
6·
(�−�)∙� �
1 2
�
1 + 1 2 + 1 4 + 1 8 + 1 16 ……
1 2
� ∙ (� − �) ∙ � � + �
1 2
�
1 + 1 2 + 1 4 + 1 8 + 1 16 ……
1 2

















