
25
3. Figurtall, følger og rekker - Perlebrett
Det trengs 6 ere perler fra gur til gur, sett vekk fra gur 1. Derfor velger vi å endre nummereringen.
Størrelse/Figur
Antall i den ytterste ringen Økning fra forrige ledd
Vi velger ny nummering
1
1
2
6
5
a
1
= 6
3
12
6
a
2
= 12
4
18
6
a
3
= 18
5
24
6
a
4
= 24
6
30
6
a
5
= 30
Den konstante økningen viser at antall perler per ring, tilsvarer en aritmetisk følge.
Vi kan bruke formelen for aritmetisk rekke. Til slutt må man addere 1, dvs. midtperlen som man har tatt
bort under beregningen.
1
1
6
6
( 1)
6 6( 1) 6
n
n
a
d
a a d n
a
n
n
=
=
= + −
= + − =
Aritmetisk rekke for antall perler til et brett med størrelsen
n
:
1
2
(
)
2
(6 6 ) (3 3 ) 3 3
2
n
n
n
n s
a a
n s
n n n n n
= +
= + = + = +
Svaret med midtperlen:
2
3 3 1
n n
+ +
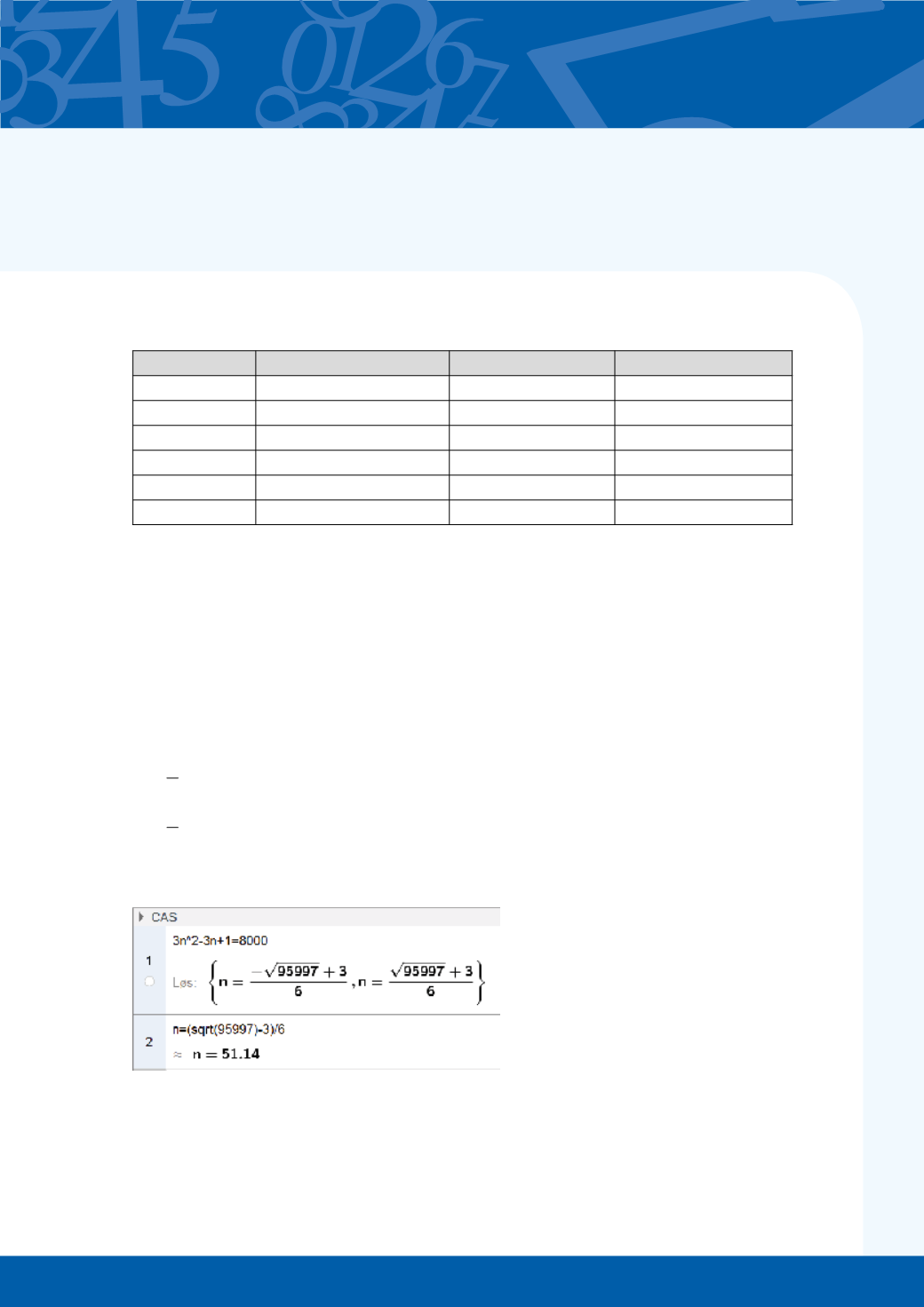
• Hvor stort perlebrett kan vi lage med 8000 perler?
NB!
Her må vi huske at vi nummererte tallene på ny. Vi må altså addere 1 for å nne nummeret til
perlebrettet. Se svaret under aktivitet 3.
Med 8000 perler kan man lage gur 52.

















