Basic HTML Version
100
First, we seek a model for (the average) R
G
of flexible chains, similar to those
of spheres and rods.
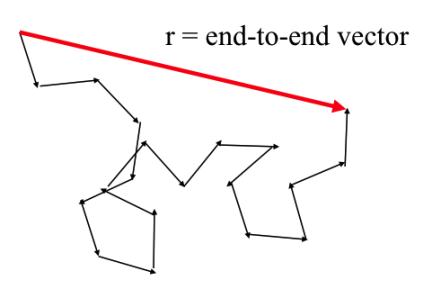
The simplest case: A vector model (Figure 13) describes a freely jointed chain
with no restrictions on the direction (random orientation)
Figure 45
There are n vectors (representing monomers), each of length l. (Note that n
∝
M). As a useful intermediate quantity we first determine the average square
end-to-end distance: <r
2
> (which is not the same as <r>
2
).
For a sufficiently high number of vectors i.e. a very long chain, the following
applies:
r
2
=
nl
2
(
n
→ ∞
)
r
=
0
Note the average end-to-end distance (<r>) is zero because since all end-to-
end vectors cancel pairwise since they are equally probable. However, the
average squared end-to-end distance (<r
2
>) is always positive. And
represents a useful parameter for the extent of chain expansion.
The relation <r
2
> = nl
2
(for large n values) can be proven in a very elegant
way, starting with recognizing that r
2
must be the dot product of the end-to-
end vector
r
by itself, since the angle between the vectors is zero (cos
φ
= 0)

