Produktive matematiske samtaler som et utgangspunkt for å øve på kjernepraksiser

Foto: Esben Krogstad Kamstrup/NTNU

Kjernepraksis er et stort og flott ord, som brukes hyppig i forbindelse med lærerutdanning. Men hva er egentlig en kjernepraksis? Og hvordan kan man arbeide med kjernepraksiser i lærerutdanning?

I rammeplanen for den femårige lærerutdanninga har det skjedd en dreining fra tidligere rammeplaner: fra å fokusere på undervisningskunnskap, hva en lærer skal og bør kunne, til å fokusere på oppgaver en lærer gjør, og at lærerstudenter skal ha mulighet til å øve på noen slike kjernepraksiser (Mosvold, Fauskanger og Wæge, 2018). En kjernepraksis er definert av Grossman, Hammerness og McDonald (2009) som noe en lærer gjør regelmessig og som fremmer elevers læring. I rammeplanen for matematikkfaget i lærerutdanninga finner vi flere kjernepraksiser, blant annet at lærere skal inkludere alle elever i matematisk resonnering og argumentering, stimulere til kritisk matematisk tenking og legge til rette for meningsfulle matematiske samtaler med og mellom elever. I matematikk på lærerutdanninga for 1. til 7. trinn har vi arbeidet med en undervisningsaktivitet som skal gi studenter mulighet til å øve på kjernepraksiser.

Lampert og kollegaer (2013) foreslår arbeid med en syklus av utprøving og utforskning (se Figur 1) for at studenter skal få anledning til å øve på noen kjernepraksiser, og det er en slik syklus vi har fått utdanningskvalitetsmidler fra Institutt for lærerutdanning til å arbeide med i emnet Matematikk 1 som det undervises i ved grunnskolelærerutdanninga 1-7.

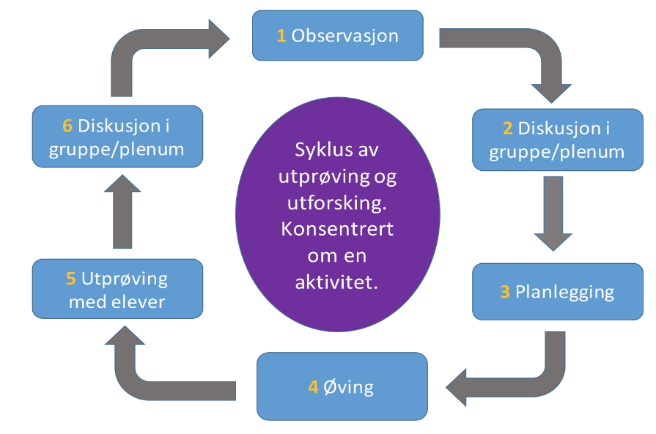
1. Observasjon av en gitt aktivitet med elever, ev. på film
2. Diskusjon om aktiviteten
3. Studenter planlegger en lignende aktivitet med elever
4. Studenter øver på aktiviteten i gruppa gjennom rollespill
5. Studenter prøver ut aktiviteten med en elevgruppe, andre observerer og bidrar ved behov
6. Diskusjon

Syklusen er sentrert rundt en matematisk samtale omkring en matematisk aktivitet, i vårt tilfelle oppgavestrenger (for mer om oppgavestrenger, se f.eks. Valenta (2016)) som skal åpne opp for å fremheve og begrunne regnestrategier i multiplikasjon. De to første fasene har vi jobbet med i undervisningstida til faget, der vi har sett video av liknende sykluser fra MAM-prosjektet, før vi i grupper med ca. åtte studenter og én lærerutdanner reiser ut til en barneskole for å gjennomføre de neste fire fasene av syklusen. I planleggingsfasen planlegger studentene og lærerutdanneren en samtale omkring en matematisk sammenheng i detalj, både hvilke spørsmål de vil stille, hvilke representasjoner de de vil bruke, og hvordan de kan sørge for å øke elevenes deltakelse. Etter at samtalen er planlagt, trekkes én student til å gjennomføre samtalen. Først øver gruppa på samtalen i fellesskap, der de andre studentene og lærerutdanneren spiller rollen som elever, og deretter gjennomføres opplegget med elever. Under utprøvingen med elever, har alle studentene og lærerutdanneren ansvar for at samtalen blir slik de har planlagt. Vi sikrer at hele gruppa tar ansvar for undervisningsopplegget ved at både den som gjennomfører, men også resten av gruppa, kan be om time out underveis. Ved time out kan gruppa stille spørsmål til hverandre, og diskutere hvordan de skal gå frem videre for å opprettholde en produktiv samtale. I etterkant av utprøvingen reflekterer gruppa over samtalen. Vi har transkribert videoopptak fra noen planleggingsfaser, og nå vil vi gi et lite innblikk i hvordan planleggingsfasen i en syklus kan foregå.

Gruppa planlegger en samtale omkring en oppgavestreng i multiplikasjon, der målet for samtalen er å fremheve og begrunne regnestrategien som går ut på at man kan dele opp den ene faktoren i et multiplikasjonsstykke (eksempel: 6⋅32=6⋅25+6⋅7). I utdraget under ser vi at studentene foreslår ulike regnestrategier som kan benyttes for å regne ut 6⋅25, der Student 4 benytter seg av regnestrategien som er målet for økta:

Utsagn 23: Student 4 -Jeg starta først med å gange 6 ganger 5, og så 6 ganger 10, nei, 6 ganger 20.

Utsagn 27: Student 2 -25 pluss 25 er 50, (J: Mhm) og 50 pluss 50 er 100 (J: Mhm) da har vi brukt opp fire av dem (J: Mhm) så da legger vi på 50 til da så vi vet at vi har to igjen.

Utsang 39: Student 1 -Det var jo den 6 ganger 20 og 6 ganger 5, men så har jeg vært inne på litt halvering-dobling, da, med 3 ganger 50.

Videre diskuterer gruppa hvordan de kan begrunne regnestrategien (utsagn 159), før de diskuterer hvordan begrunnelsen kan generaliseres (utsagn 230-231):

Utsagn 159: Student 3 -Rett og slett dele opp og, hvis man har de posene med 25 i da, så er det jo veldig enkelt å se for seg at man tar ut fra ene posen, også putter det i en ny pose, og da tar du ut fem stykker, og så sitter du igjen med 20 drops i hver pose, og de seks av posene, også har du seks poser med fem i hver, det er veldig enkelt å visualisere da.

Utsagn 230: Student 1 -Ehm, går ikke det an å begrunne det med at den mengden du fordeler altså totalen vil alltid, altså det er viktig at det alltid er det samme og at du fordeler den mengden i like mange deler.

Utsagn 231: Student 2 -Vi deler opp mengden, og så regner vi ut hver for seg, og så legger vi sammen de regnestykkene.

En av kjernepraksisene vi nevnte innledningsvis var stimulere til kritisk matematisk tenkning, og ved å planlegge en samtale som handler om ikke bare utregning, men også begrunnelse og generalisering, får studentene anledning til å øve på denne kjernepraksisen. Ved at studentene har analysert det matematiske innholdet grundig selv, blir det også lettere å legge til rette for en meningsfylt matematisk samtale. Utdraget under viser et eksempel på at studentene planlegger spørsmål som skal fremme resonnering og begrunnelse, og på denne måten får de øvd på praksisen legge til rette for meningsfulle matematiske samtaler:

Utsagn 221: Student 1 -I og med at vi har to forskjellige eksempler, så går det an å spørre dem om de tror eller tenker om det her fungerer for alle tall.

Utsagn 222: Jo -Og så sier de ja.

Utsagn 223: Student 1 -Også da eventuelt spørre hvorfor eller hva vi har lært som gjør at dem blir…

Den siste av praksisene vi nevnte innledningsvis var inkludere alle elever i matematisk resonnering og argumentering, og denne praksisen kan vi se at gruppa jobber med i utdraget under, der de legger til rette for nabosnakk:

Utsagn 103: Jo -Ja, okei, her er neste oppgave. Seks ganger 25. Nå er vi jo over i der hvor vi kanskje kan forvente at de både trenger litt mer tid til å tenke seg om og at det kan være mer variasjon i måtene dem har tenkt på. Hva gjør vi nå da? Vi gir dem oppgaven seks ganger 25. Nå må vi komme i gang med litt sånn … Ja?

Utsagn 104: Student 2 -Kanskje de skal få snakke to og to?

Utsagn 105: Student 8 -Be dem tenke?

Utsagn 110: Student 5 -Men de kan jo kanskje tenke litt sjøl først, og gjøre seg opp noen tanker og så snakke med sidemannen, så de ikke snakker rett ifra (utydelig) selv.

Utsagn 111: Jo -Mhm. Okei, skal vi gå for det da? Seks ganger 25. Hva blir beskjeden da? «Tenk…».

Utsagn 112: Student 6 -Tenk litt selv, og så snakk sammen.

Arbeidet med syklusen av utprøving og utforskning har vært lærerikt for både studenter og lærerutdannere. Studentene har fått anledning til å øve på produktive matematiske samtaler i en situasjon der kompleksiteten i en vanlig undervisningssituasjon er redusert, og dette gir igjen muligheter for å øve på noen kjernepraksiser for matematikklærere. Lærerutdannerne har fått mye erfaring med å være veiledere under en slik syklus, og vi bruker erfaringene våre til å få enda mer ut av arbeidet med syklusen ved neste anledning.

Grossman, P., Hammerness, K., & McDonald, M. (2009). Redefining teaching, re‐imagining teacher education. Teachers and Teaching: theory and practice, 15(2), 273-289.

Lampert, M., Franke, M. L.., Kazemi, E., Ghousseini, H., Turrou, A. C., Beasley, H., Cunard, A., & Crowe, K. (2013). Keeping it complex: Using rehearsals to support novice teacher learning of ambitious teaching. Journal of Teacher Education, 64(3), 226–243.

Mosvold, R., Fauskanger, J., og Wæge, K. (2018). Fra undervisningskunnskap i matematikk til kjernepraksiser. Uniped, 41(04), 401-411.

Valenta, A. (2016). Oppgavestrenger i arbeid med tallforståelse.