När jag tittade igenom en inspelad föreläsning i mekanik, kom det en fråga från en student om Newton’s första lag (N1). Vad är den till för? Föreläsaren svarade att den var ett specialfall av Newton’s andra lag (N2). Detta fick mig att reagera och börja fundera. Hur ser vi egentligen på N1 och N2. Det som på pappret såg ut att vara en ”lätt” fråga visade sig inte vara helt enkel. Jag startar från början.
Principia, Newton’s första lag
Newtons lagar, kommer från Isaac Newton’s mästerverk ”Principia”[1], där dom formulerades ordentligt första gången. Det som bör noteras är att N1 är en omformulering av Galileo’s tröghets princip, Att ett objekt som inte utsätts för några krafter kommer att fortsätta sin rörelse i all oändlighet. Även om Newton gav Galileo fullt erkännande för N1, så är Newton’s formulering mer djupgående. Men det var inte bara Galileo och Newton som kommit fram till liknande slutsatser, Thomas Hobbes och Rene Descartes hade liknande tankar.
Newton’s första lag hittar vi i Principia under Axiom. På latin formuleras den:
Lex I: Corpus omne perseverare in statu suo quiescendi vel movendi uniformiter in directum, nisi quatenus a viribus impressis cogitur statum illum mutare.
Law I: Every body perseveres in its state of being at rest or of moving uniformly straight forward, except insofar as it is compelled to change its state by forces impressed.
Vad säger detta ”axiom” egentligen? Här kan man ha ganska många olika tolkningar, men här måste vi som Newton skriver i Principia ha ”ett öppet sinne”. Det första vi ser är att vi egentligen inte kan bevisa att den gäller. Detta då vi inte kan skapa en situation utan krafter som verkar. Det andra är att axiomet inte kan gälla i ett tomrum, vi måste kunna relatera rörelsen till något. Detta något är det vi kallar ett referenssystem, eller tröghetssystem (inertial system). Med andra ord N1 kräver att vi definierar ett tröghetssystem där N1 gäller, och som en följd gäller även de andra lagarna där. Hur kopplar man detta till Newton’s tro på ett absolut rum? Ser man till den tid då Newton levde var detta en självklarhet, vilket gjorde att han ansåg detta som självklart men N1 har dock inte detta som ett krav.
Det står klart att N1 är mycket viktigare än man egentligen undervisas. I majoriteten av böckerna som jag tittat i kommer man mycket snabbt till en matematisk formulering av N1: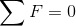
och en kort diskussion om tröghetssystem. Se Generell fysikk[2] eller University Physics [3] som exempel. Den matematiska formulering gör det svårt att särskilja den från den vanligaste formuleringen av N2.
Newton’s andra lag
Newton’s andra lag, som följer den första formulerades:
Lex II: Mutationem motus proportionalem esse vi motrici impressae, et fieri secundum lineam rectam qua vis illa imprimitur.
Law II: A change of motion is proportional to the motive force impressed and takes place along the straight line in which that force is impressed.
För att kunna tolka denna måste vi se till Newtons definitioner:
Definition I: Quantity of matter is a measure of matter that arises from its density and volyme jointly.
Definition II: Quantity of motion is a measure of motion that arises from the velocity and the quantity of matter jointly.
Definition IV: Impressed force is the action exerted on a body to change its state either of resting or of moving uniformly straight forward.
Vi ser att Newton använder sig av rörelsemängden (bevegelsemengde) när han talar om rörelsen, inte accelerationen. Dessutom är kraften som läggs på momentant och inte kontinuerlig (som för den sakens skull är ett special fall). Detta gör att en direkt översättning av N2 till modern matematisk formulering blir:
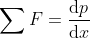
Vilket inte är den vanligaste formen att presentera N2. Generell fysikk [2], University Physics [3] använder istället:
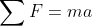
Vilken introducerades av Euler i mitten av 1700-talet.
Det är notabelt att The Feynman lectures on Physics [4] och Fundamental University Physics [5] använder den förra.
Vad är fördelen? Det uppenbara är att man inte direkt kan se N1 som ett special fall av N2. Dessutom får man fördelen av att kunna använda sig av momentana krafter direkt och kan generalisera till kontinuerliga krafter. Att sedan rörelsemängden är en bevarad storhet gör inte situationen sämre.
Slutord.
Den tankeprocess som en kommentar och ett svar i en videoinspelning startade, fick mig dels till att gå tillbaka till ursprunget och dels att fundera på hur och vad det är vi undervisar i fysik. Föreläsaren är troligen inte den ende som inte fullt ut har förstått vad Newton’s lagar egentligen säger. Detta beror på att många läroböcker inte presenterar dom på ett korrekt sätt. Man väljer oftast ett sätt som kanske är det pedagogiskt riktiga men som gör att den djupa förståelsen för grundläggande principer blir lidande.
Med tanke på att det tog nästan 200 år efter publiceringen av Principia innan man fick en definitivt klargörande av det epistemologiska innehållet i Newton’s första lag, så är det kanske inte så konstigt att vi använder oss av den utan att till fullo tagit till oss vad den säger. Det är lite av ”Shut up and calculate” och hur N1 behandlas, något som är synd då den är viktig i behandlingen av den speciella relativitetsteorin.
[1] I. Newton, Mathematical Principles of Natural Philosophy, I.B. Cohen & A Whitman, eds. (University of California Press, Berkely 1999)
[2] J.R. Lien& G. Løvhøiden, Generell fysikk for universiteter og høgskoler, bind 1 Mekanikk. (Universitetsforlaget, Oslo 2010)
[3] H. D. Young, & R. A. Freedman. Sears and Zemansky’s university physics. 13ed , (Pearson education, 2012)
[4] R.P. Feynman, R. B. Leighton, & M. L. Sands. The Feynman lectures on physics: Mainly mechanics, radiation, and heat. Vol. 1. (Addison-Wesley , 1963).
[5] M. Alonso & E. J. Finn. Fundamental university physics. Vol 1. (Addison-Wesley, 1968).