Optimization of transmit ultrasound pulses in second harmonic imaging
Today, Second harmonic imaging is a preferred ultrasound imaging modality, mainly due to its ability to improve image quality by suppressing undesired acoustic reverberations (Averkiou et al, 2000). This imaging modality improves the diagnostics for different medical applications. Most of the cardiac ultrasound scanners in the hospitals use this method. The principle is as follows: the scanner transmits an ultrasound pulse at a specific fundamental frequency (f0). Then, nonlinear propagation in human tissue generates a second harmonic signal component at double the fundamental frequency. Finally, echoes at the second harmonic frequency (2f0) are received and used to construct the ultrasound image.
This second harmonic method assumes that all second harmonic signal is generated during propagation through tissue. Therefore, it requires very good control of the transmit pulse so that no signal at the second harmonic frequency is transmitted by the ultrasound probe (also referred to as transducer). However, due to the intrinsic nonlinearity of pulser electronics in an ultrasound scanner and/or in an ultrasound probe, some undesired second harmonic component still appears in the emitted pulse.
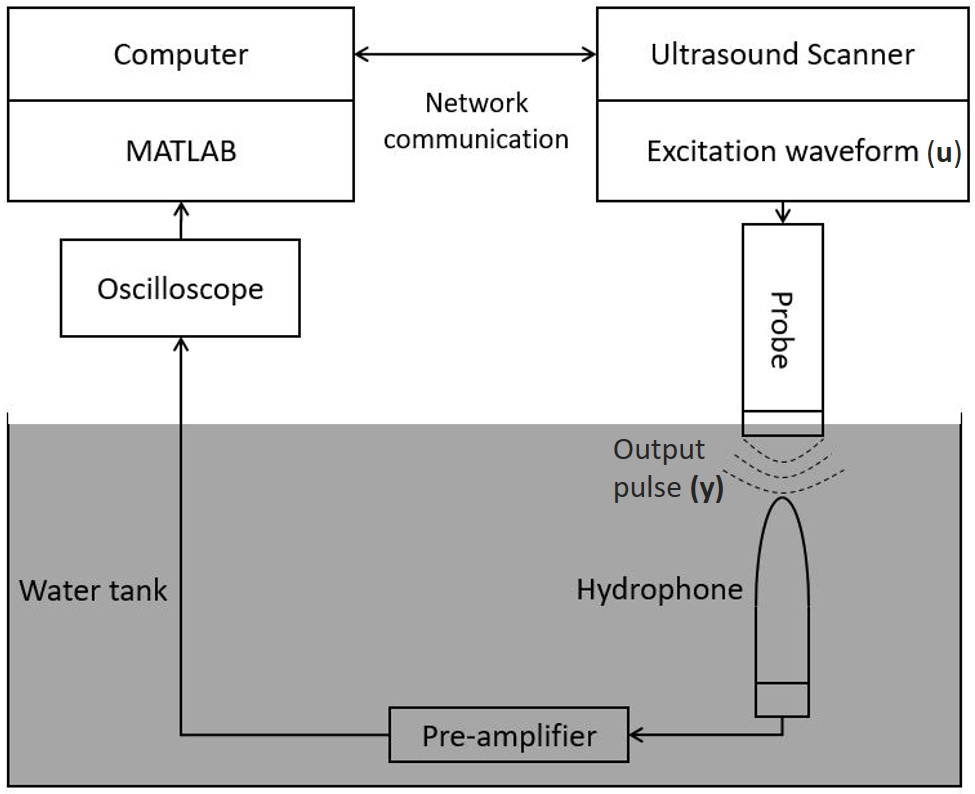
In our research project, we established an experimental measurement system to measure, manipulate, and optimize excitation waveforms for second harmonic imaging. One of the goals is to reduce the undesired transmitted second harmonic signal to below -30 dB of the fundamental frequency signal. An optimization procedure was used to automatically measure and compensate for the undesired nonlinearity in the transmit system, finding a pre-distorted controlling electrical excitation waveform that produces an ultrasound transmit pulse without second harmonic signal components.
The optimization framework is illustrated in Figure 1. Transmitted ultrasound pulses were measured in a water tank using a hydrophone, which is an underwater microphone. The pulses were measured close to the transducer surface, at a distance of approximately 3 mm, before harmonics from nonlinear propagation in water had developed. A computer program first evaluates the second harmonic signal content in the measured pressure pulses, then runs an optimization algorithm to refine the input excitation waveform, to subsequently send it to the ultrasound scanner via a network connection. The scanner uses this new waveform to transmit a new output pulse (y) which was again measured with the hydrophone. This procedure was repeated for a preset number of iterations.
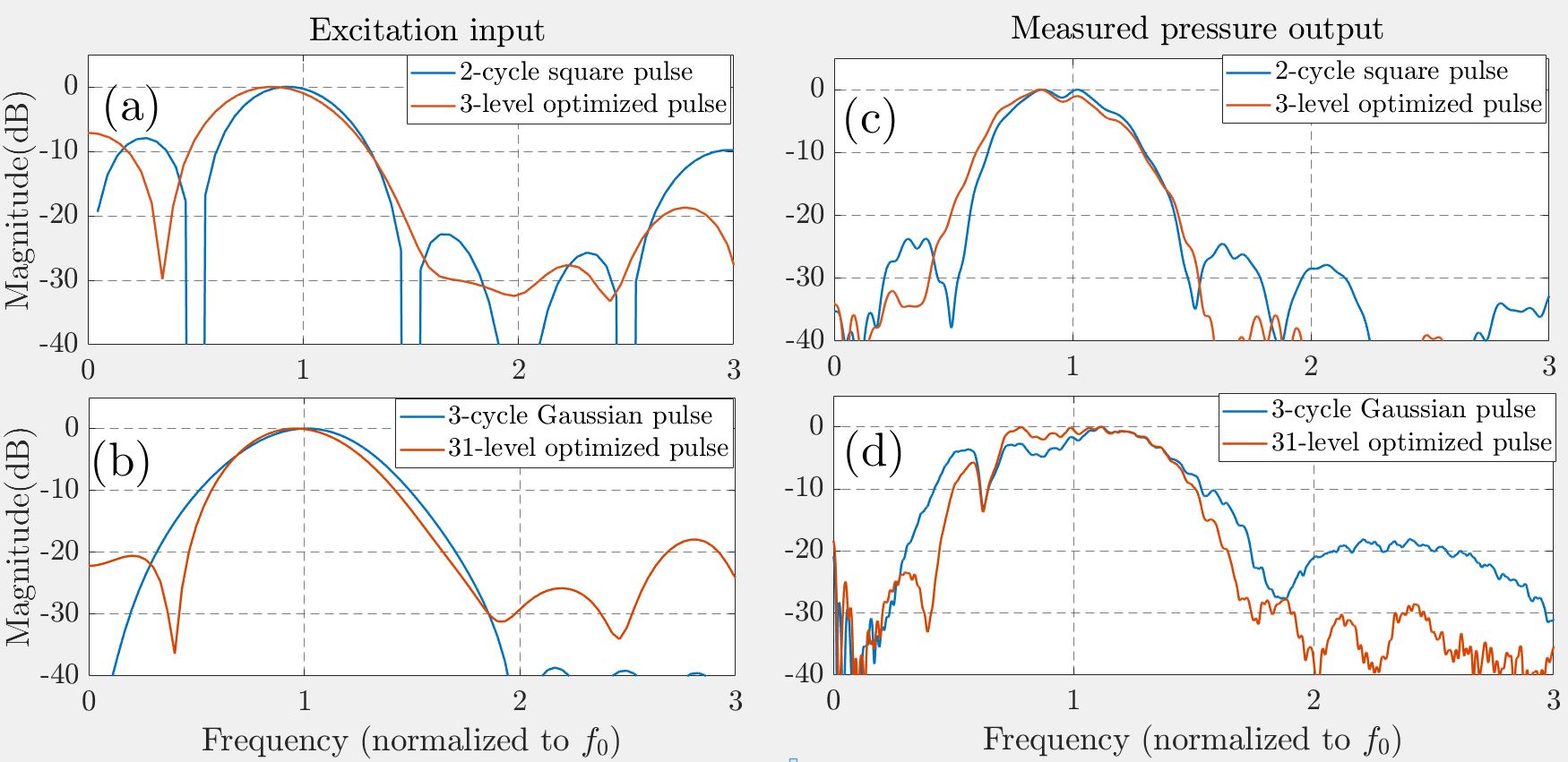
The method was applied to optimize for two different set-ups: one with an ultrasound transducer electrically driven by a 3-level pulser, and one with another transducer type that was driven by a 31-level pulser. Figure 2 shows the electrical input and pressure output pulses for both set-ups in the frequency domain. As an illustration, these results are compared with two typical excitations with the same pulse length: a 2-cycle square wave for the 3-level pulser and a Gaussian-modulated sinusoidal wave for the 31-level waveform. Using the excitations found by this method, the measured transmitted second harmonic levels are 40 dB and 30 dB lower than the fundamental for the 3-level and 31-level pulser respectively. Moreover, the second harmonic level is about 15 dB lower, which is better, than the two typical (uncompensated) excitation waveforms.
Figure 2 shows that the optimized excitation waveforms contain more energy at the second harmonic band than the two typical waveforms do, while the resulting ultrasound output pulses contain less second harmonic signal. This illustrates how the optimization process works on the measured ultrasound pulses: the transmitted second harmonic is reduced by adding some second harmonic signal component at a different phase to the input pulses, counteracting nonlinear effects in the whole system, e.g. quantization errors and nonlinearity in the driving electronics and/or transducer.
Thong Huynh
- This author does not have any more posts.