One probe, two frequencies – numerical optimization of dual-frequency transducers
At the heart of any ultrasound system, lies the transducer. The transducer is used for applications ranging from creating images of foetuses and disintegrating kidney stones (lithotripsy), to detecting cracks in gas pipes. Without it, the world at large would be a different place. See this blog post for an introduction to the transducer: Improvements in ultrasound transducer design and manufacturing.
The numerous medical applications of ultrasound each demands a specific operating frequency that vary from 0.5 MHz to 100 MHz. For example, for cardiac imaging, a trade-off between resolution and the distance to the object is negotiated and frequencies in the range 2 MHz to 5 MHz is commonly used. If smaller objects situated closer to the transducer are imaged, higher frequencies are used. Ophthalmology and small animal imaging use frequencies that may extend to 20 MHz. High-intensity focused ultrasound, hereby referred to as ultrasound surgery, permits incision-free surgery by heating tissue within a small region, and uses frequencies in the kilohertz range.
In a perfect world, there would be one ultrasound probe for all applications. However, due to the resonating properties of the active piezoelectric material used in ultrasound probes, this is not realistic. Ultrasound probes are therefore designed to work at around 60-100% of the operating frequency.
If ultrasound probes were designed to operate at two different frequencies, say, 0.5 MHz for ultrasound surgery and 4 MHz for imaging, the physicians could have real-time images of the tissue being treated. The physician would then be able to determine whether the ultrasound therapy beam actually hits the target, as well as providing estimates as to the treatment progress. This idea is of course not new, and today, the combination of imaging and ultrasound therapy may be performed using costly MRI. A combined ultrasound and imaging probe is expected to decrease the cost of such an operation.
Another new and interesting technology intended for cancer treatment is the Acoustic Cluster Therapy (ACT) developed by Phoenix Solution, see the blog post Microbubbles and focused ultrasound cure tumours in mice. The technology demands the use of two different frequencies at approx. 0.5 MHz and 2 MHz. As of today, to perform the in-vivo studies, two separate transducers have been used. However, if the technology is advanced to patient treatment, the use of two transducers may be cumbersome for the clinicians to work with.
An ultrasound transducer that permits the use of two, or more, separate frequencies is referred to as a dual-frequency transducer. Typically, to obtain one transducer capable of operating at two different frequencies, two piezoelectric disks are used, each with their own operating frequency. The major challenge with dual-frequency probes is to make them perform optimally for both frequencies. Due to the expected complexity in optimizing dual-frequency transducers, we at the Centre of Innovative Ultrasound Solutions (CIUS) have chosen to investigate if numerical optimization methods can be used.
A numerical method allows the transducer to be treated as a black box; instead of an analytical description of the transducer, so-called target functions are used to optimize the transducer. The optimization is performed by repeated 1D simulations of a transducer structure where a selected set of material or structural parameters are changed stochastically until a given target function is satisfied.
We have developed a numerical optimization method for ultrasound probes that has been accepted as a conference proceeding at the 2017 IEEE International Ultrasonics Symposium (IUS). The method optimizes a transducer to transmit short pulses, which is crucial in ultrasound imaging applications.
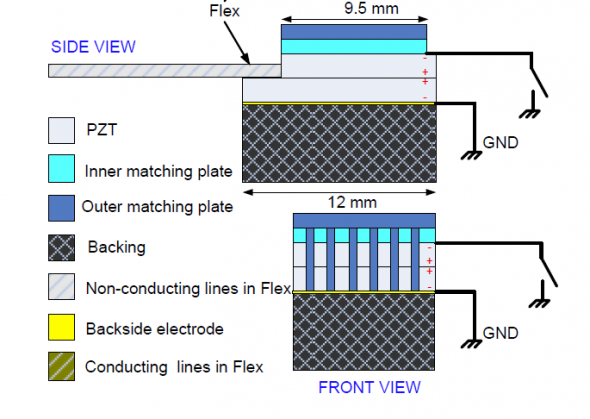
An example of a dual-frequency transducer optimized with the numerical method is shown in Figure 1. This is a continuation of the work performed by my colleague Tung Manh and can be found here: Design and prototyping of dual layer linear arrays. The application for this transducer may be 2nd and/or 3rd harmonic imaging, or a dual-mode of operation where the low and high frequency band may be used interchangeably. The transducer consists of two piezoelectric layers where both layers are used for the low frequency band, while only the bottom layer is used for the high frequency band.
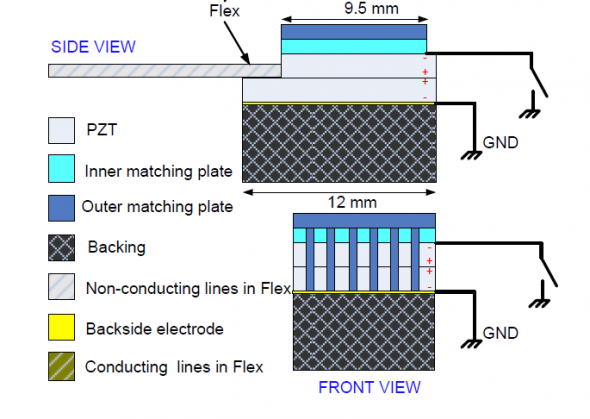
In Figure 2, simulation results of the optimized transducer is shown where we compare the optimized dual-frequency transducer with a conventional transducer using only one piezoelectric layer. At first glance, we see that the dual-frequency transducer exhibits a lower sensitivity compared to the conventional transducer. This is of course unwanted and can largely be explained by differences in the backing material. However, and most importantly, the dual-frequency transducer’s high frequency band spans further than the conventional transducer’s frequency band and operation at 6 MHz is feasible.
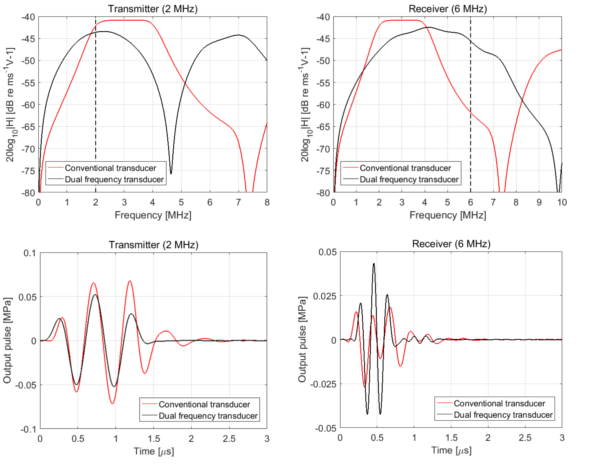
In conclusion, dual-frequency transducers have a great potential. However, due to the wave nature of ultrasound energy, optimizing a transducer for two, or more, separate frequencies is challenging; often one frequency band is prioritized over the other. A numerical optimization method may find optimal solutions for both frequencies; however, such a solution might still be less optimal than a conventional transducer designed for only one frequency band. Nevertheless, as already mentioned, new usages of ultrasound (ACT) and the combination of imaging and ultrasound surgery may demand the use of two separate frequency bands, and using two transducers for a dual-frequency operation is not feasible in all cases.

Kenneth K. Andersen
- This author does not have any more posts.